Argomento: Equilibrio di un sistema rigido
Se un corpo è soggetto a due o più forze, la loro somma vettoriale, cioè la forza risultante, produce da sola lo stesso effetto dell' insieme delle singole forze. Tale effetto complessivo di un sistema di forze non dipende solo dalla somma vettoriale delle forze, ma anche dai punti in cui le singole forze sono applicate.
Per esempio una singola forza agisce procurando al corpo cui è soggetta un moto traslatorio lungo la direzione della forza stessa. Una coppia di forze applicata ad un corpo crea un momento torcente in punti differenti può invece provocare un moto rotazionale attorno ad un asse perpendicolare al piano in cui agiscono le forze come in figura:

Generalmente l’ effetto delle forze produce sia un moto traslazionale, sia un moto rotazionale si dice che il corpo ha un moto rototraslazionale.
La condizione di equilibrio di un corpo è quindi legata alle forze che agiscono su di esso, ma anche ai momenti delle forze stesse. Certamente le condizioni necessarie per l'equilibrio sono che la somma vettoriale delle forze sia nulla, perchè in caso contrario un corpo inizialmente fermo verrebbe messo in movimento, e che il momento delle forze agenti sul corpo sia complessivamente nullo, perché altrimenti il corpo verrebbe messo in rotazione.
Queste due condizioni possono essere espresse dalle equazioni

dette anche equazioni cardinali. La condizione sulle forze permette l’ equilibrio traslazionale, quella sui momenti l’ equilibrio rotazionale.
ESPERIMENTO 3: EQUILIBRIO DI UNA GUIDA OMOGENEA
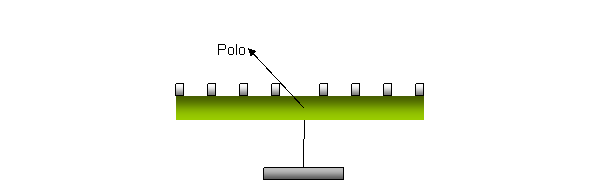
Una guida omogenea è incernierata in un punto , chiamato polo o fulcro, che si trova sulla verticale del centro di massa. Il polo costituisce il centro di simmetria intorno a cui la guida può ruotare. L’ unico moto possibile per la guida è quello rotazionale, in quanto il vincolo al quale la guida è incernierata impedisce un moto di traslazione.
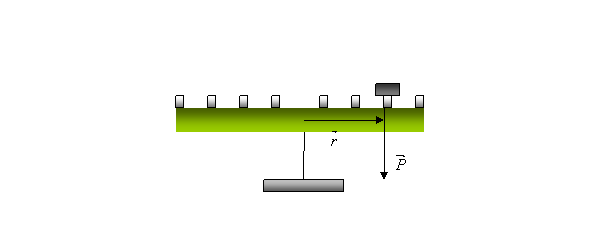
Se su una parte della guida, inizialmente in equilibrio in posizione orizzontale, viene aggiunto un pesetto di peso ![]() , si viene a creare un momento pari
, si viene a creare un momento pari ![]() con modulo
con modulo ![]() , dove r è la distanza tra il polo (centro di massa e di rotazione ) ed il punto in cui viene applicato il pesetto
, dove r è la distanza tra il polo (centro di massa e di rotazione ) ed il punto in cui viene applicato il pesetto
Il momento crea una rotazione della guida omogenea attorno al suo centro di rotazione. Per avere l’ equilibrio è necessario che vi sia una forza dall’ altra parte della guida che crei un momento ![]() di pari intensità e direzione al precedente ma di verso opposto. Poiché per le equazioni cardinali deve sussistere la relazione
di pari intensità e direzione al precedente ma di verso opposto. Poiché per le equazioni cardinali deve sussistere la relazione ![]() è necessario porre un pesetto uguale alla stessa distanza dal polo dalla parte opposta della guida, oppure un peso P1 ad una distanza r1 per cui risulti
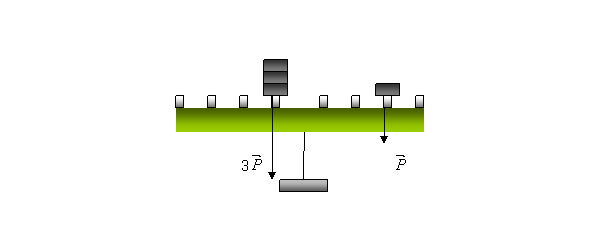
è necessario porre un pesetto uguale alla stessa distanza dal polo dalla parte opposta della guida, oppure un peso P1 ad una distanza r1 per cui risulti ![]() . Per esempio se il peso P è posizionato a 3 unita di lunghezza sulla destra rispetto al polo, si può equilibrare la guida posizionando un peso 3P ad 1 unità di lunghezza sulla sinistra
. Per esempio se il peso P è posizionato a 3 unita di lunghezza sulla destra rispetto al polo, si può equilibrare la guida posizionando un peso 3P ad 1 unità di lunghezza sulla sinistra