Algoritmo di Huffman
Alla fine degli anni 40, agli albori della Teoria dell'Informazione, nuove ed efficienti tecniche di codifica cominciavano ad essere scoperte ed i concetti di entropia e ridondanza venivano introdotti.
L'entropia è una misura dell'incertezza con la quale un testo viene prodotto da una sorgente (per esempio un fax, un modem ecc.).
Ciò che in quegli anni si proponeva di realizzare, vista l'assenza di elaboratori elettronici, era definire degli algoritmi che riuscissero a codificare testi in modo che questi potessero essere inviati da una sorgente ad una destinazione senza che nessuno, tranne il destinatario, potesse carpirne il contenuto oppure algoritmi che potessero permettere al destinatario di capire se un testo codificato fosse stato trasmesso con errori, dovuti alla trasmissione o ad un sabotaggio da parte di terzi. Nasce in tal modo il concetto di codice e di codifica.
Un codice può essere visto come una tabella con due colonne: la prima colonna contiene i caratteri contenuti nel testo originario, la seconda contiene le parole di codice.
Codificare un testo significa sostituire ciascuna parola (o carattere) del testo originario con la corrispondente parola di codice presente nella tabella del codice.
Un codice è univocamente decodificabile se è possibile decodificare ogni carattere del testo in input in modo univoco.Nell'ambito dei codici univocamente decodificabili è possibile riconoscere i codici prefissi.
Un codice è prefisso se è possibile decodificare correttamente una parola di codice non appena essa è riconosciuta nel testo codificato T, poiché nessuna parola di codice è prefisso di un'altra parola di codice. In generale una parola W è prefisso di un'altra parola W' se W' = Wa. Di seguito è mostrato un esempio di codice prefisso a lunghezza variabile
| Carattere |
Parola codice |
| A |
00 |
| B |
01 |
| C |
10 |
| D |
110 |
| E |
111 |
Se il testo codificato è T = 0001111, allora scorrendo T si riconosce dapprima il carattere A, quindi, il carattere B ed infine il carattere E, per cui il testo decodificato sarà ABE.
Una codifica, d'altronde, è una regola che associa ad ogni carattere (o parola) del testo una parola di codice.
Con l'avvento dei moderni calcolatori elettronici si è sviluppato parallelamente alla teoria dei codici il concetto di compressione dati. Supponiamo di avere a che fare con un testo su di un file: ogni carattere viene rappresentato da una stringa di 8 bit, quindi se riuscissimo a codificare un carattere utilizzando meno di otto bit, sarebbe possibile diminuire lo spazio occupato dal testo originale. Utilizzando i concetti di entropia e ridondanza è stato possibile sviluppare algoritmi capaci di risalire alla codifica di un carattere, conoscendone il numero di occorrenza in un dato testo in modo tale da ridurre la taglia complessiva del testo stesso.
E possibile affermare che il primo di tali algoritmi è stato l'algoritmo proposto da C. Shannon e R. M. Fano.
E' importante ricordare che, fissato un codice, affinché esso sia efficiente, deve accadere che parole di codice associate a caratteri meno frequenti siano costituite da più bit, mentre parole di codice associate a caratteri più frequenti siano costituite da meno bit.
Nel 1951 a David Huffman e ad un suo collega al corso del MIT di Teoria dell'Informazione venna data la scelta tra una tesi scritta o un esame. Il docente, Robert M. Fano, assegnò una tesi sul problema di trovare il codice binario più efficiente. Huffman, incapace di dimostrare un qualsiasi codice che fosse il più efficiente, si stava rassegnando all'idea di dover studiare per l'esame, quando gli venne l'idea di usare un albero binario ordinato in base alla frequenza, e così dimostrò velocemente che questo metodo era il più efficiente.
Un'idea simile era stata usata in precedenza nella Codifica di Shannon-Fano (creata da Claude Shannon, inventore della teoria dell'informazione, e Fano, il docente di Huffman!), ma Huffman sistemò la sua più grande lacuna costruendo un albero ascendente anziché uno discendente.
La codifica di Huffman usa un metodo specifico per scegliere la rappresentazione di ciascun simbolo, risultando in un codice senza prefissi (cioè in cui nessuna stringa binaria di nessun simbolo è il prefisso della stringa binaria di nessun altro simbolo) che esprime il carattere più frequente nella maniera più breve possibile. È stato dimostrato che la codifica di Huffman è il più efficiente sistema di compressione di questo tipo: nessun'altra mappatura di simboli in stringhe binarie può produrre un risultato più breve nel caso in cui le frequenze di simboli effettive corrispondono a quelle usate per creare il codice.
Ecco un esempio: Vogliamo comprimere un file testo contenente la stringa: CIAO_MAMMA
In un normale file testo, ogni lettera è rappresentata da 8 bits codificati rispettando il codice ASCII. Le lettere dell'esempio verrebbero quindi codificate nel modo seguente:
A = 01000001
C = 01000011
I = 01001001
O = 01001111
M = 01001101
_ = 00100000
Il nostro file salvato sarà composto così da 80 bits, ovvero 10 lettere * 8 bit.
01000011 01001001 01000001 01001111 00100000 01001101 01000001 01001101 01001101 01000001 |
| Adesso applichiamo l'algoritmo di Huffman per calcolare dei nuovi codici da assegnare alle lettere dell'esempio. Il metodo usato è piuttosto semplice. Si deve costruire un albero in cui le lettere più frequenti siano posizionate più vicino alla radice rispetto a quelle con minore frequenza. |
Per prima cosa è necessario contare la frequenza di ogni lettera nella nostra stringa:
C(1) I(1) A(3) M(3) O(1) _(1)
|
1.Analizza il numero di ricorrenze di ciascun elemento costitutivo del file da comprimere: i singoli caratteri in un file di testo, i pixel in un file grafico. |
| A questo punto vanno individuate le 2 lettere con minore frequenza. Nel nostro caso, le lettere con minore frequenza sono ad esempio la C e la I, che useremo per costruire un nuovo nodo alla base dell'albero.
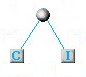
Il nodo costituito dalle 2 lettere di minor frequenza: C ed I
Nel nostro schema delle frequenze, la C e la I saranno da ora in avanti rappresentate come un unica lettera e con una frequenza che sarà la somma delle loro frequenze:
C+I(2) A(3) M(3) O(1) _(1)
|
2.Accomuna i due elementi meno frequenti trovati nel file in una categoria-somma che li rappresenta entrambi. Così ad esempio se A ricorre 8 volte e B 7 volte, viene creata la categoria-somma AB , dotata di 15 ricorrenze. Intanto i componenti A e B ricevono ciascuno un differente marcatore che li identifica come elementi entrati in un'associazione. |
Troviamo nuovamente le due lettere con minore frequenza (O e _) e facciamo la stessa cosa...
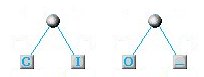
Il nodo costituito dalle 2 lettere di minor frequenza O e _
C+I(2) A(3) M(3) O+_(2)
A questo punto cerchiamo ancora le 2 lettere con minor frequenza e vediamo che si tratta dell'accoppiata C+I e O+_ per cui il nuovo nodo sarà schematizzato usando i nodi creati in precedenza:
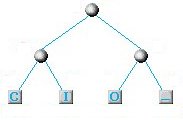
Il nodo costituito dalle 2 lettere di minor frequenza: C+I e O+_
Lo schema diventerà a questo punto il seguente:
C+I+O+_(4) A(3) M(3)
Prendiamo ancora una volte le 2 lettere di minor frequenza che adesso sono la A e la M:
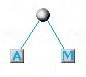
Il nuovo nodo costituito dalle 2 lettere di minor frequenza: A e M
Il nostro schema a questo punto si ridurrà a 2 soli elementi:
C+I+O+_(4) A+M(6)
|
3.L'algoritmo identifica i due successivi elementi meno frequenti nel file e li riunisce in una nuova categoria-somma, usando lo stesso procedimento descritto al punto 2. Il gruppo AB può a sua volta entrare in nuove associazioni e costituire, ad esempio, la categoria CAB . Quando ciò accade, la A e la B ricevono un nuovo identificatore di associazione che finisce con l'allungare il codice che identificherà univocamente ciascuna delle due lettere nel file compresso che verrà generato. |
| Dovendo prendere le due lettere con minor frequenza non ci rimane che selezionare le uniche due rimaste e concludere finalmente il nostro albero:
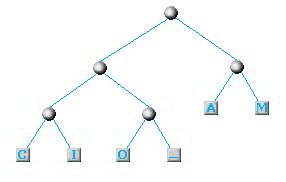
L'albero nella sua versione finale (o quasi)
|
4. Si crea per passaggi successivi un albero costituito da una serie di ramificazioni binarie, all'interno del quale appaiono con maggiore frequenza e in combinazioni successive gli elementi più rari all'interno del file, mentre appaiono più raramente gli elementi più frequenti. In base al meccanismo descritto, ciò fa sì che gli elementi rari all'interno del file non compresso siano associati ad un codice identificativo lungo, che si accresce di un elemento ad ogni nuova associazione. Gli elementi invece che si ripetono più spesso nel file originale sono anche i meno presenti nell'albero delle associazioni, sicché il loro codice identificativo sarà il più breve possibile. |
| Una volta creato l'albero, bisogna associare ad ogni nodo un bit. E' possibile associare lo 0 a tutti i nodi di sinistra e 1 a tutti quelli di destra. E' possibile anche fare il contrario senza compromettere il risultato finale. Nel nostro caso scegliamo lo 0 a sinistra e l'1 a destra ed ecco il risultato finale:
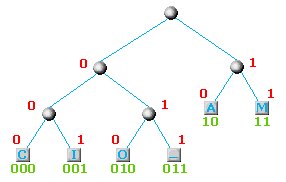
L'albero con i relativi bit associati e con i valori (in verde) assegnati ad ogni singola lettera.
Volendo scrivere a questo punto il nostro CIAO_MAMMA con i nuovi codici otterremo la seguente sequenza di bits:
000001100100111110111110
Solamente 24 bits invece degli 80 usati in precedenza con il codice ASCII ! E solamente su una stringa di 10 caratteri. Immaginiamo lo stesso algoritmo applicato ad un file testo di migliaia di parole per capirne la vera potenza. |
5.Viene generato il file compresso, sostituendo a ciascun elemento del file originale il relativo codice prodotto al termine della catena di associazioni basata sulla frequenza di quell'elemento nel documento di partenza. |
E' importante sottolineare che il codice ottenuto non è univoco, nel senso che può essere creato un codice altrettanto valido ma differente dal nostro che può dipendere ad esempio dalle lettere con minore frequenza scelte all'inizio oppure dal modo in cui decidiamo di impostare gli 0 e gli 1 sui rami dell'albero.
Una caratteristica particolare di questo algoritmo è che il codice ottenuto per ogni singola lettera NON è un prefisso di un altra lettera. Nel nostro esempio, la A ha il codice 10 e nessuna altra lettera ha una codifica che comincia con 10 (lo stesso ovviamente vale per ogni altra lettere che abbiamo codificato). In questo modo leggendo la stringa di 24 bits che abbiamo ottenuto in precedenza, possiamo riconoscere le singole lettere senza bisogno di un separatore tra loro.
000001100100111110111110
CCCIIIAAOOO___MMAAMMMMAA
|
Il guadagno di spazio al termine della compressione è dovuto al fatto che gli elementi che si ripetono frequentemente sono identificati da un codice breve, che occupa meno spazio di quanto ne occuperebbe la loro codifica normale. Viceversa gli elementi rari nel file originale ricevono nel file compresso una codifica lunga, che può richiedere, per ciascuno di essi, uno spazio anche notevolmente maggiore di quello occupato nel file non compresso.
Dalla somma algebrica dello spazio guadagnato con la codifica breve degli elementi più frequenti e dello spazio perduto con la codifica lunga degli elementi più rari si ottiene il coefficiente di compressione prodotto dall'algoritmo Huffman. Da quanto detto si deduce che questo tipo di compressione è tanto più efficace quanto più ampie sono le differenze di frequenza degli elementi che costituiscono il file originale, mentre scarsi sono i risultati che si ottengono quando la distribuzione degli elementi è uniforme.
Un'ottima dimostrazione del funzionamento di questo algoritmo è visionabile su Internet all'indirizzo http://www.cs.sfu.ca/CC/365/li/squeeze/Huffman.html. Qui troverete un'applet java in grado di eseguire la generazione dell'albero delle associazioni, di produrre il codice compresso e di calcolare il coefficiente finale di compressione. Nelle due immagini sotto riportate, tratte dall'uso di questa applet, potete osservare l'albero generato dalla frequenza di ricorsività delle lettere costituenti un noto scioglilingua ed il risultato della compressione Huffman ottenuta.
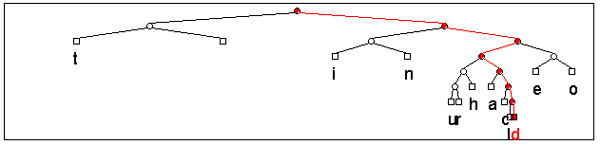
L'albero delle associazioni relativo al testo di uno scioglilingua. La struttura dell'albero mostra che le lettere d
e l
sono le meno frequenti di tutte

La compressione ottenuta ha permesso un risparmio di spazio pari a quasi il 60%







